【目標】
●有効数字の概念を理解する
●有効数字の計算を完璧にできるようにする!
化学では「有効数字○桁で答えよ」という計算問題を避けて通ることができない。そんな中で有効数字をよく分からずにここまで来ている人は多いのではないだろうか。
先生目線では授業時間が足りず、カットされがちな項目であり、
生徒目線では「今更質問しづらいし…」ということが多々あるように感じる。
そんな悩みを解消すべく、本ページを読めば有効数字は完璧となるコンテンツを提供する。
有効数字とは
実験をするとき、「目盛りを読む」という人間の目分量がはたらき、これを測定値という。
実験では必ず目盛りの10分の1まで読むという原則があり、読めた数値を有効数字という。
(アナログの例)定規で長さを読む
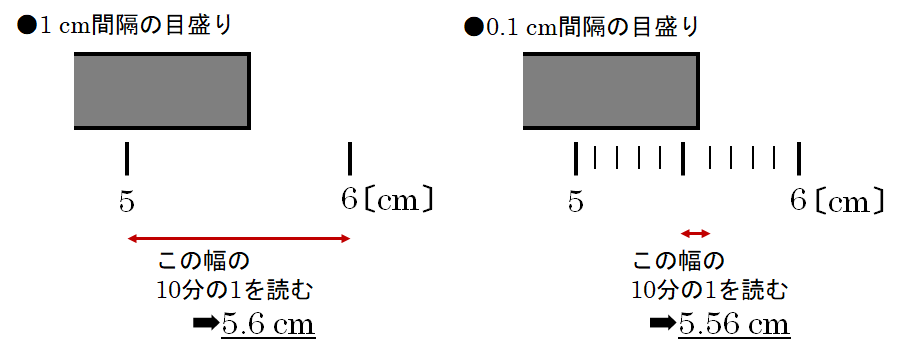
このように目盛り間隔が違うだけで、読む数値が変わります。また、目盛りが細かいほど精度を上がることが分かりますね。また右の例では、私は5.56 cmとしましたが、見る人によっては5.55 cmや5.57 cmと読む人がいるかもしれません。どうしても人によって感じ方が異なるのでブレるのです。
同じ物体なので長さは変わらないはずですが、測定道具によって数値が変わるのが分かります。このように測定値にはブレがあり、読んだ数値は実際とは少しずれている可能性があることを念頭に置く必要があります。数学ではピッタリの数字ですが、化学などの測定値を扱うときは精度とブレに注意しなければなりません。よって化学において「5」と「5.0」と「5.00」はまったくの別物となります。有効数字は一番下の桁は信用できない(ブレる)という認識を持ちましょう。よって化学において「5.00」と書いてあるものについて、小数点第1位以下を勝手に切り捨てて「5」と表記するのはナンセンスということになります。
| 測定値 | 有効数字 | 数値の意味 |
|---|---|---|
| 5 | 1桁 | 5±1(4~6) |
| 5.0 | 2桁 | 5.0±0.1(4.9~5.1) |
| 5.00 | 3桁 | 5.00±0.01(4.99~5.01) |
よって「5.00」と書いてあるものについて、小数点第1位以下を勝手に切り捨てて「5」と表記するのはナンセンスということになります。
有効数字の桁数の数え方
「0.325」の有効数字は何桁ですか?
「4桁!」と答えた人は残念ながら数え方を理解していません。
授業をしていても、有効数字の読み方をきちんと理解していない人が多いと感じますので、今一度整理しましょう。
【有効数字の桁数の数え方】
①一番左(大きい位)の数字から見る。この数字が「1~9」であれば1桁目と数える。※「0」であれば数えず、右隣の数値を見に行く。
≪※部分について≫
(一番左の数字が「0」であるとき)一つ下の位の数字を見る。この数字が「1~9」であれば1桁目と数える。※「0」であれば数えず、右隣の数値を見に行く。以降1桁目と決定できるまでくり返す。
②1桁目が決まったら以降はどの数値でも(「0」であっても)一つ下の位が2桁目、さらに一つ下の位が3桁目、…とし、書かれている一番右(小さい位)数値まで桁数を決定する。
③最後に読んだ桁が有効数字○桁の「○」に入る。
問 次の数字の有効数字は何桁か答えよ。
(1) 1.4
(2) 0.300
(3) 0.00201
解答解説
(1) 1.4
一の位が「1」であり、「1~9」の数字であるため1桁目となる。
以降「4」が2桁目と読み終了。 ⇒ 2桁
A. 2桁
(2) 0.300
一の位が「0」であり、桁数にカウントしない。
小数第一位が「3」であり、「1~9」の数字であるため1桁目となる。
以降小数第二位の「0」が2桁目、小数第三位の「0」が3桁目と読み終了。⇒ 3桁
A. 3桁
(3) 0.00201
一の位が「0」であり、桁数にカウントしない。
小数第一位が「0」であり、桁数にカウントしない。
小数第二位が「0」であり、桁数にカウントしない。
小数第三位が「2」であり、「1~9」の数字であるため1桁目となる。
以降小数第四位の「0」が2桁目、小数第五位の「1」が3桁目と読み終了。⇒ 3桁
A. 3桁
有効数字計算の3ルール
今後、有効数字どうしを計算して数値を求める機会が出てきます。ブレがあるものを足す、かけるなどするため、さらにブレが大きくなります。信用できない数値を多く残してもしょうがないため、計算する際は次の3つのルールに従って楽に計算できるようにしましょう。
【有効数字計算の3ルール】
ルール① 足し算引き算は有効数字の末尾が最も左側(=最も位が大きいもの)に合わせる。最も左から一つ下の位を四捨五入する。
ルール② 掛け算割り算は最小の有効数字の桁数に合わせる。その桁数から一つ下の位を四捨五入する。
ルール③ 連続した計算で最終的に有効数字n桁を求めたい場合、途中計算はn+1桁まで求め(n+2桁以降は切り捨て)、最後の計算はn+1桁を四捨五入する。
問 次の計算を有効数字に気を付けて答えよ。
(1) 2.31 g+17.682 g+35.3 g
(2) 2.32 cm×1.431 cm
(3) 2.32 cm×1.431 cm その後算出した面積に高さ1.27 cmを掛けて体積を出す
解答解説
(1) 2.31 g+17.682 g+35.3 g

今回は「35.3 g」が測定した中で数値が存在する位が大きく、一番精度が低い(35.2~35.4 gの範囲)ため、他の小数第二位、第三位を足して残しても、誤差となる。これによって小数第二位を四捨五入して決定する。
A. 55.3 g(有効数字3桁)
(2) 2.32 cm×1.431 cm

3桁と4桁の掛け算のため、小さい桁数の「3桁」にする。
計算結果が出たため、1桁多い「4桁目」を四捨五入して決定する。
A. 3.32 cm2(有効数字3桁)
(3) 2.32 cm×1.431 cm その後算出した面積に高さ1.27 cmを掛けて体積を出す

A. 4.13 cm3(有効数字3桁)
まとめ
【有効数字の桁数の数え方】
①一番左(大きい位)の数字から見る。この数字が「1~9」であれば1桁目と数える。※「0」であれば数えず、右隣の数値を見に行く。
≪※部分について≫
(一番左の数字が「0」であるとき)一つ下の位の数字を見る。この数字が「1~9」であれば1桁目と数える。※「0」であれば数えず、右隣の数値を見に行く。以降1桁目と決定できるまでくり返す。
②1桁目が決まったら以降はどの数値でも(「0」であっても)一つ下の位が2桁目、さらに一つ下の位が3桁目、…とし、書かれている一番右(小さい位)数値まで桁数を決定する。
③最後に読んだ桁が有効数字○桁の「○」に入る。
【有効数字計算の3ルール】
ルール① 足し算引き算は有効数字の末尾が最も左側(=最も位が大きいもの)に合わせる。最も左から一つ下の位を四捨五入する。
ルール② 掛け算割り算は最小の有効数字の桁数に合わせる。その桁数から一つ下の位を四捨五入する。
ルール③ 連続した計算で最終的に有効数字n桁を求めたい場合、途中計算はn+1桁まで求め(n+2桁以降は切り捨て)、最後の計算はn+1桁を四捨五入する。









